算法设计与分析课后作业

第一讲[200225]

练习题

1.用伪代码写出求整数最大公因子的欧几里得算法

GCD(a,b)

r=a%b
If b=0 
Then Return b
Else Return GCD(b,r)    

2.考虑如下伪代码

F(n)

1 if n=1

2 then return 1

3 else return n* F(n-1)

这是计算n！的算法

3.时间复杂度是否是衡量一个算法性能的主要标准，为什么？

是的，时间复杂决定了执行一个算法的时间资源，那么对选择算法与选择设备有极大的参考意义

4.包含死循环的程序是不是算法，为什么？

不是算法。因为对于一些输入，它不会停下来。

5.是否可以通过提高算法的时间复杂性来降低其空间复杂性？

这是可以的。比如桶排序，虽然时间复杂性非常低，但是空间复杂性很高，那么我们可以改成虽然时间复杂度高一点的快速排序，来节约空间。

思考题

在信息产业中算法扮演什么角色？

信息产业中的算法，就好像人的灵魂，指导信息产业的前进。

第二讲[200227]

练习题

1.证明或否证：f(n)+o(f(n))=Θ(f(n))

根据o(f(n))定义，$\forall c>0,\exists n_0, \forall n>n_0, 0\le o(f(n))< cf(n),因此f(n)\le f(n)+o(f(n))< (1+c)f(n), 故f(n)\le f(n)+o(f(n))\le (1+c)f(n)$，所以f(n)+o(f(n))=Θ(f(n))

2.证明：Θ(f(x)) + O(g(x)) = O(max(f(x), g(x)))

根据定义有，

$$\exists c_1,c_2>0,x_0,\forall x>x_0,c_1f(x)\le \Theta(f(x))\le c_2f(x)\\ \exist c>0, x_1,\forall x>x_1,0\le O(g(x))\le cg(x)$$

因此

$$\forall x>max(x_0,x_1)\\ 0\le c_1f(x)\le \Theta(f(x))+O(g(x))\le c_2f(x)+cg(x)\le(c_2+c)(max(f(x),g(x)))$$

故Θ(f(x)) + O(g(x)) = O(max(f(x), g(x)))

3. 证明或给出反例：Θ(f(n))∩o(f(n))=∅

用反证法证明。假设存在$g(n)\in \Theta(f(n))\bigcap o(f(n))$，则根据定义

$$\exists c_1,c_2>0,x_0,\forall n>n_0,c_1f(n)\le g(n)\le c_2f(n)\\ \forall c>0,\exists n_1,\forall n>n_1,0\le g(n)< cf(n)$$

然而对于$c<c_1$该结论显然不成立，矛盾。因此原命题正确。

4.证明：设k是任意常数正整数，则logkn = o(n)

即证明$\forall c>0,\exist n_0,\forall n>n_0,0\le \log_kn<cn$ 那么对于任意的k，我们取$n_0=\frac{1}{c\ln k}$，根据单调性，结论显然成立。

5.证明：logn!=Θ($n\log n$)

$$\log n!=\sum_{i=1}^n\log i\le n\log n$$

则结论显然成立。

6.用迭代法解方程 T(n)＝T(9n/10)+n

$$T(0)=0\\ T(n)=T(0.9n)+n=n+0.9n+T(0.9^2n)=n\sum_{i=0}^\infty0.9^i+T(0)=10n$$

7. 解方程 T(n)=6T(n/3)+logn

令$S(n)=T(3^n)$ 则$S(n)=T(3^n)=6T(3^{n-1})=6S(n-1)+n$ 从而$S(n)是一个整数列S_0=T(1)=$

8.解方程 T(n) =3T(n/3 +5) + n/2

考虑到n很大时，5可以忽略，我们使用Master定理。$a=3,b=3,\epsilon =0.001,f(n)=\frac{n}{2}$，那么$n^{\log_ba}=n,f(n)=\Theta(n^{\log_ba})$ 因此T(n)=$\Theta(n\lg n)$

9.解方程 T(n)= T($\lceil\frac{n}{2}\rceil)$+1

向下取整不影响使用Master定理。$a=1,b=2,\epsilon =1,f(n)=1$，那么$n^{\log_ba-\epsilon}=n=O(n)=f(n)$ 因此T(n)=$\Theta(n^2)$

10.解方程 T(n)=9T(n/3)+n

使用Master定理。$a=9,b=3,\epsilon =0.001,f(n)=n$，那么$n^{\log_ba}=n^2;f(n)=1=\Theta(1)$ 因此T(n)=$\Theta(\lg n)$

11.解方程 T(n)=T$(\lfloor\frac{n}{2}\rfloor)$+$n^3$

向上取整不影响使用Master定理。$a=1,b=2,\epsilon =3,f(n)=1$，那么$n^{\log_ba+\epsilon}=n^3=\Omega(n^3)=f(n)$，且对于所有充分大的n有$f(\frac{n}{2})<f(n)$， 因此T(n)=$\Theta(n^3)$

12.证明或否证：如果f(n)=O(g(n))，那么2f(n)=O(2g(n))

由f(n)=O(g(n))知

$$\exist c>0, n_0,\forall n>n_0,0\le f(n)\le cg(n)$$

那么

$$0\le 2f(n)\le c\cdot 2g(n)$$

即2f(n)=O(2g(n))

13.令f, g和h为定义在正整数上的正实数函数。假设f(n)=O(g(n))，g(n)=O(h(n))，证明f(n)=O(h(n))

由f(n)=O(g(n)),g(n)=O(h(n))知

$$\exist c>0, n_0,\forall n>n_0,0\le f(n)\le cg(n)\\ \exist c'>0, n_1,\forall n>n_1,0\le g(n)\le c'h(n)$$

那么

$$0\le f(n)\le cg(n)\le cc'h(n)$$

即f(n)=O(h(n))

14.将下列函数按它们在n→∞时的无穷大阶数，从小到大排序

$$n,n^{\lg 7},n^{2.5},n^3\log n,n^2\log n,n\log n$$ $$n^{\lg 7} \lt n \lt n \log n\lt n^2\log n\lt n^{2.5}\lt n^3\log n$$

15.一个时间复杂性为O($n^2$)的算法的运行时间一定大于一个时间复杂性为O(n)的算法么？为什么？

不一定。如果n足够小，而O(n)算法的常数很大，那么反而可能是$O(n^2)$算法较快。

思考题

维基百科中的Master定理描述和算法导论不同，思考其差别以及哪个正确？

两个定义是等价的。

第三讲[200303]

1.给定平面上n个点，求其中的一点对，使得在n个点的所有点对中，该点对的距离最小。严格地说，最接近点对可能多于1对。为了简单起见，这里只限于找其中的一对。

1 设计一个时间复杂度为O($n^2$)的算法求距离最近的点对，要求写出算法伪代码

d_min=Infty;
p1=null,p2=null
input Set<Point> P
while P.Count>1 :
    p=P.RemoveFirst()
    for q in P:
        d=CalculateDistance(p,q)
        if (d_min>d)
            d_min=d
            p1=p
            p2=q

2 利用分治的思想设计一个时间复杂度为O($n\log n$)的算法求距离最近的点对，要求写出算法伪代码。

d_min=Infty;
p1=null,p2=null

(int, Point, Point) GetMinDistance(Set<Point> P):
    if (P.Count<=1) return Infty
    if (P.Count==2) 
        return CalculateDistance(p.First(), p.Last())
    m=P.GetMedian(p => p.X)
    P1=P.Select(p => p.X<=m)
    P2=P.Select(p => p.X>m)
    (d1,p11,p12)=GetMinDistance(P1)
    (d2,p21,p22)=GetMinDistance(P2)
    d_min=Min(d1,d2)
    if(d1=d_min)
        p1=p11
        p2=p12
    else
        p1=p21
        p2=p22
    Pm=P.Select(p => Abs(p.X-m)<d_min)
    while Pm.Count>1 :
    p=Pm.RemoveFirst()
    for q in Pm:
    dm=CalculateDistance(p,q)
    if (d_min>dm)
        d_min=dm
        p1=p
        p2=q
    return (d_min,p1,p2)

2.对于平面上的两个点p1=(x1, y1)和p2=(x2,y2)，如果x1<=x2且y1<=y2，则p2支配p1，给定平面上的n个点，请设计算法求其中没有被任何其他点支配的点。

input Set<Point> P
P.

3.设计一个分治算法，在一个2维平面上求n个点中距离最近的两个点，要求时间复杂性是o($n^2$)，请写出算法伪代码并分析时间复杂性。

4.阅读https://oi-wiki.org/math/quick-pow/学习基于分治思想的“快速幂”算法。设计一个通过矩阵运算，在O(logN)时间内计算斐波那契数列第N项的算法。

5.给定一个数组A，任务是设计一个算法求得数组中的“主元素”，即在数组中个数超过数组总元素个数一半的元素。但是数组中元素的数据类型可能是复杂类型，这意味着数组中的元素进能够比较是否相等而不存在序关系，设对于两个元素A[i]和A[j]，判定是否A[i]=A[j]需要常数时间。

1 设计一个时间复杂性为O(n log n)的算法解此问题

2 设计一个时间复杂性为O(n)的算法解此问题.

6.对于给定的n个元素的数组A[1..n],要求从中找出第k小的元素。请设计分治算法解决这个问题，要求算法的平均时间复杂度是O(n)。答案要求包含以下内容：（1）用简明的自然语言表述算法的基本思想；（2）用伪代码描述算法；（3）分析算法的时间复杂度。

7.给定实数数组A[1:n]，试设计一个分治算法找出其中的最小元素和最大元素，使得比较操作的总次数严格小于2(n-1)。答案要求包含以下内容：（1）用简明的自然语言表述算法的基本思想；（2）用伪代码描述算法；（3）分析算法的时间复杂度。

8.有长度为N的数组A、B，每个数组中存储的浮点数已经升序排列。设计一个O(logn)时间的分治算法，找出这2n个数的中位数。证明算法的正确性。

9.设计分治算法求解下述问题：

输入：一个一维整数数组A(其中元素可能是正数也可能是负数) 输出：A的连续子数组，要求其和最大 例如，输入数组是{-2, -5, 6, -2, -3, 1, 5, -6}，其结果是{6, -2, -3, 1, 5},其和为7. 要求: (1) 算法时间复杂度为O($n\log n$)；(2) 写出算法伪代码；(3) 分析算法时间复杂度

第四讲[200305]

1.设计一个“三路归并”的排序算法，并分析它的时间复杂性。

2.Hadamard矩阵$H_0,H_1,H_2,\cdots$递归定义如下

$H_0$是矩阵[1];

对于k>0, Hk是$H_k是2^k\times 2^k$的矩阵

$$\left[ \begin{matrix} H_{k-1} & H_{k-1}\\ H_{k-1} & -H_{k-1} \end{matrix} \right]$$

设v是一个长度为$2^k$的列向量，设计一个时间复杂性为O($n\log n$)的算法计算矩阵-向量乘法$H_kv$(设单个数字的加法和乘法都在单位时间内完成)。

3.已知在一个$2^k\times2^k$（k>0）个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。

如 所示的特殊棋盘为k=2时的一个特殊棋盘。 现在要用 4种不同形态的L型骨牌覆盖一个给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。 （1）利用分治的思想设计一个算法解决棋盘覆盖问题； （2）分析该算法的时间复杂度。

4.假设建筑表示为三元组$(x_L,H,x_R)$，其中$x_L,x_R$表示建筑左、右两侧的x坐标,H表示建筑的高度。

如 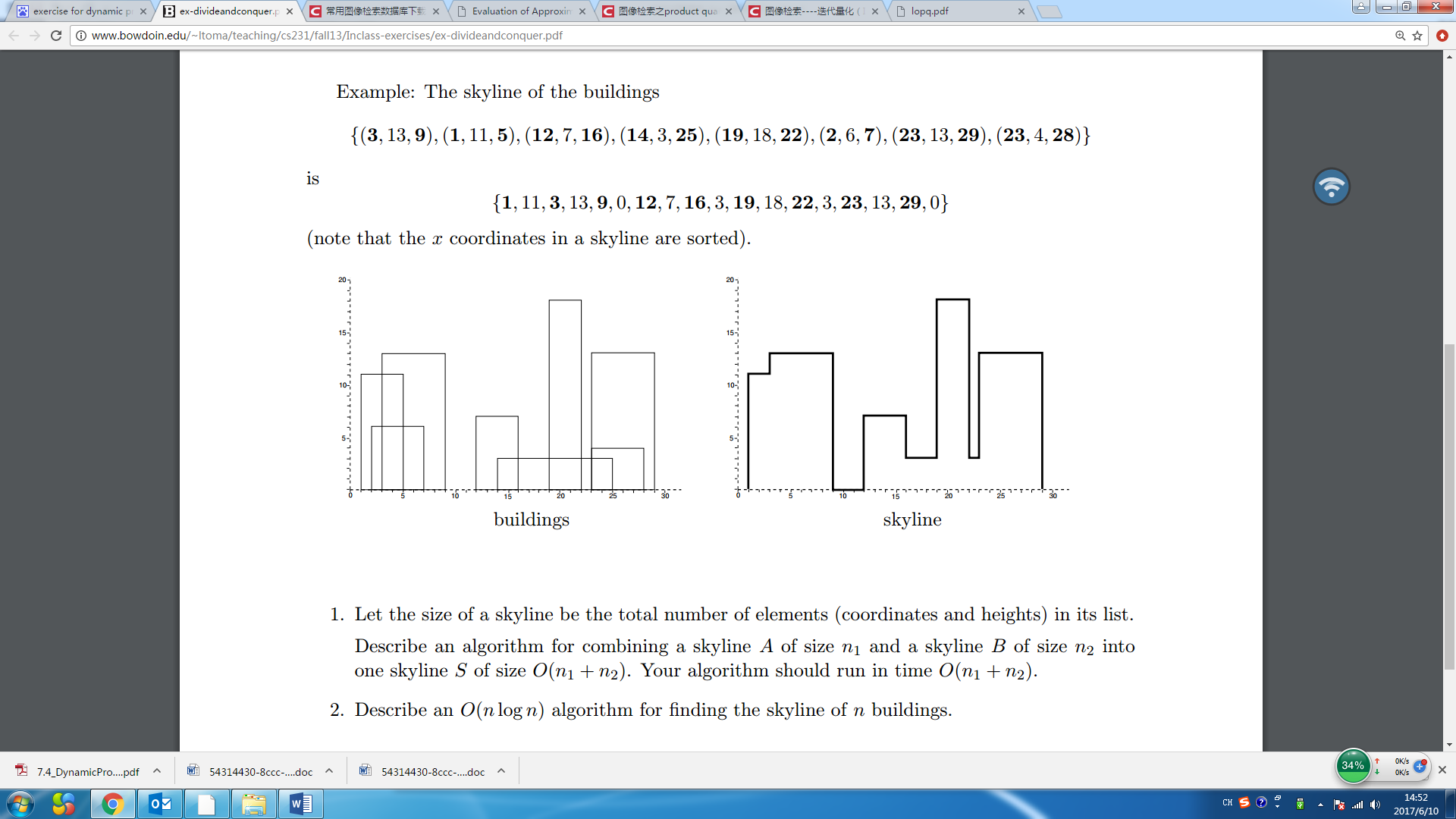中的建筑可以表示为三元组序列{(3, 13, 9),(1, 11, 5),(12, 7, 16),(14, 3, 25),(19, 18, 22),(2, 6, 7),(23, 13, 29),(23, 4, 28)。建筑群的skyline是一系列横坐标以及连接相邻横坐标的水平线高度来表示，下图右侧的skyline表示为整数序列(1, 11, 3, 13, 9, 0, 12, 7, 16, 3, 19, 18, 22, 3, 23, 13, 29, 0)。考虑设计分治算法求解如下计算问题。给出分治算法的伪代码描述，并分析算法的时间复杂度。 问题定义：输入：n幢建筑构成的建筑群；输出：n幢建筑的skyline;

5.逆序对数求解：有长度为N的浮点数组A，元素分别为a1, a2, ..., aN。如果满足i<j且ai>aj，则(ai, aj)构成一个逆序对。设计分治方法求解数组A的逆序对个数，并分析算法的时间复杂性。

6.给定一棵有N个节点的树，树上的每条边都有权值。定义两个节点vi, vj间的距离dis(vi, vj)为节点间路径的权值和。设计分治方法求解：树上有多少个节点对(vi, vj)满足i<j、且dis(vi, vj)<=K。

7.线段树（segment tree）是用来存放给定区间（segment, or interval）内对应信息的一种数据结构。树上的每个节点代表一个区间，节点的左右子树二分地将区间分为两部分。在一棵线段树上，可以在O(logN)时间内完成“单点数据修改”、“区间最值查询”、“区间求和查询”等操作。通过阅读相关资料，理解线段树的基本工作原理后，请尝试设计一种线段树上的“区间修改算法”，使其可以在O(logn)时间内完成“对一个区间内每个数都增加一固定值”的操作，并仍能使“区间最值查询”、“区间求和查询”操作能够在O(logN)时间内完成。

第五讲[200310]

1.判断下列说法的正误 (T/F)

1. 对n个数进行插入排序的最好运行时间是O($n^2$)。
2. $n\log n$=O($n\log n$)。
3. 快速排序问题平均时间复杂性的上界是O($n\log n$)。
4. 最坏情况下，快速排序的时间复杂性是O($n^2$) 。
5. 只对于NP-难问题才有设计近似算法的必要。
6. 排序问题的下界是O(n)。
7. QuickSort的最好时间复杂度与该算法时间复杂度的数学期望是同阶函数。
8. 插入排序的运行时间是$\Omega$(n)。
9. 用基于比较的排序对5个数字排序，最坏情况下最少比较的次数是6次。
10. 最坏情况下，归并排序的时间复杂性是O($n^2$)。
11. 排序问题的上界是O($n\log n$)，其中n是待排序元素个数。
12. 快速排序是最快的排序算法。
13. 快速排序一定比归并排序更快。
14. 随机化快速排序是舍伍德算法。

2.以下排序算法中，最坏情况下时间复杂性为o($n^2$)的包括

A. 快速排序 B.归并排序 C.插入排序 D.冒泡排序

3.请比较快速排序和归并排序的优劣。

4.设计一个对7个元素进行排序的方法，保证其平均比较次数最少，要求证明这个结论

5.在N（约100000）个数中找出最小的K（约100）个数，应该采用哪种排序算法？请叙述算法过程。

6.一个问题A的时间复杂性下界为$\Omega(n^2)$，求解A的某个算法的最坏情况下时间复杂性为O($n^2$), 对于问题A没有继续研究的价值了么？为什么?

7.证明下列随机选择算法的复杂性的数学期望是O($n\log n$)

1. 均匀等可能地在S中随机抽取一个样本y;
2. 比较S中每个元素, 把S划分为如下两个集合: $$S_1=\{x|x\in S, x\lt y\}\\ S_2=\{x|x\in S, x\gt y\}$$
3. 递归地排序$S_1,S_2$;
4. 顺序输出排序的$S_1,y,S_2$

8.给定平面上n个白点和n个黑点，试设计一个分治算法将每个白点与一个黑点相连，使得所有连线互不相交，分析算法的时间复杂度。（提示：划分时类似于GrahamScan 算法考虑极角，确保子问题比较均匀）